The“Game of Life” was invented in 1970 by John Conway, a British mathematician. The rules of the game are simple, but the resulting behavior of the system that results is often surprising and in any event difficult to predict. There’s a great deal of information available online relating to this game and many implementations of it exist. I found an article called Life with XAML from 3 years ago by Scott Allen that got me started quickly getting something working in WPF. I was led to Scott’s article by Mark Betz’s blog, which has a series on his work in this space and which also led me to the Life Lexicon, which describes many of the patterns that exist in these systems (and their names).

The game runs through a series of iterations. In each iteration, all of the “cells” in the system are evaluated based on two very simple rules:

• Living cells remain alive if exactly 2 or 3 of the neighboring cells are alive.
• Dead cells come alive if three of the neighboring cells are alive.

I was actually led to this game through my investigation of Langton’s Ant, which Micah Martin used in a code kata I described in my last post. The creation of the grid for Conway’s Life in WPF will work quite well for a Langton’s Ant simulator – more to come on that.

When the game begins, the cells are randomly arrayed, with green cells representing living cells and empty cells representing dead/vacant cells. After a few iterations, the random jumble gives way to certain patterns:

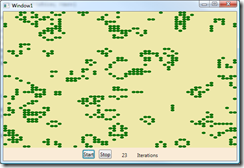
As the game continues, certain common patterns emerge and are stable unless acted upon from outside. For instance, a 2×2 square of living cells is a stable structure provided no other living cells come adjacent to it.

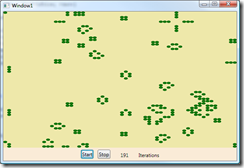
Typically, as the game progresses, the total number of living cells dwindles as it gets closer to an equilibrium state. Often it may appear as though the game is about to end, when suddenly and unexpectedly a group of cells will brush up against another pattern and give rise to a huge blossom of activity that delays the eventual end many iterations into the future.

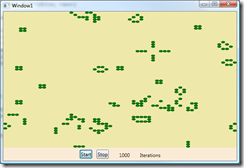
After about 1000 iterations, many of the stable formations are present.

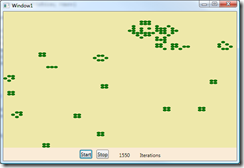
At 1500 iterations, the only activity remaining occurs in the northeast quadrant, where a green swarm of cells continues to move about.

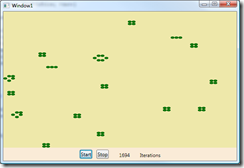
Not long after, this particular simulation ends. 2×2 squares dominate the surviving cell patterns, while 1×3 rods oscillate back and forth between horizontal and vertical orientations and a few larger structures of up to 6 cells can be seen. Much larger stable structures (with cool names) can be found at the Life Lexicon web site, and some of these can move about in predictable fashions, giving rise to the idea that this kind of theory could support the creation of nano-factories that could construct microscopic machines one atom at a time. I recently read Michael Crichton’s Prey, which is an entertaining book about just this kind of thing (and what might happen if learning swarms of nanites were to exist in the real world, rather than simply in computer memory).

Download Source(very rough at this point – eventually it will support Langton's Ant)